

图中绿色的点就是我们要预测的那个点,假设 K=3。那么 KNN 算法就会找到与它距离最近的三个点(这里用圆圈把它圈起来了),看看哪种类别多一些,比如这个例子中是蓝色三角形多一些,新来的绿色点就归类到蓝三角了。

但是,当 K=5 的时候,判定就变成不一样了。这次变成红圆多一些,所以新来的绿点被归类成红圆。从这个例子中,我们就能看得出 K 的取值是很重要的。 明白了大概原理后,细节主要有两个,K 值的选取和点距离的计算。
KNN 算法中使用的是欧式距离。二维空间两个点的欧式距离计算公式如下:

其实就是计算(x1,y1)和(x2,y2)的距离。拓展到多维空间,则公式变成这样:

这样我们就明白了如何计算距离。KNN 算法最简单粗暴的就是将预测点与所有点距离进行计算,然后保存并排序,选出前面 K 个值看看哪些类别比较多。
k值是KNN算法的一个超参数,K的含义即参考”邻居“标签值的个数。 有个反直觉的现象,K取值较小时,模型复杂度(容量)高,训练误差会减小,泛化能力减弱;K取值较大时,模型复杂度低,训练误差会增大,泛化能力有一定的提高。
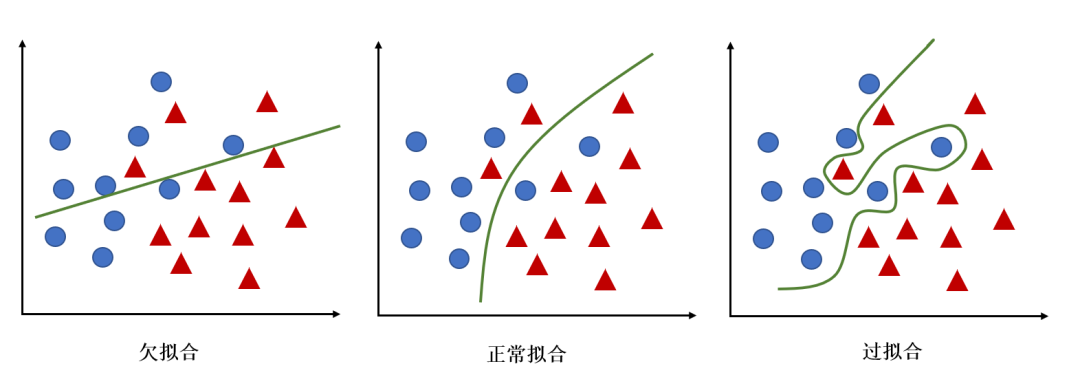
原因是K取值小的时候(如k==1),仅用较小的领域中的训练样本进行预测,模型拟合能力比较强,决策就是只要紧跟着最近的训练样本(邻居)的结果。但是,当训练集包含”噪声样本“时,模型也很容易受这些噪声样本的影响(如图 过拟合情况,噪声样本在哪个位置,决策边界就会画到哪),这样会增大"学习"的方差,也就是容易过拟合。这时,多”听听其他邻居“训练样本的观点就能尽量减少这些噪声的影响。K值取值太大时,情况相反,容易欠拟合。
通过上面那张图我们知道 K 的取值比较重要,那么该如何确定 K 取多少值好呢?答案是通过交叉验证(将样本数据按照一定比例,拆分出训练用的数据和验证用的数据,比如6:4拆分出部分训练数据和验证数据),从选取一个较小的 K 值开始,不断增加 K 的值,然后计算验证集合的方差,最终找到一个比较合适的 K 值。